Publications & Preprints
biological insight from single-cell RNA-seq data. Although cell types are naturally organized into hierarchical ontologies, most
computational models do not explicitly incorporate this structure into their training objectives. We introduce a hierarchical
cross-entropy loss that aligns model objectives with biological structure. Applied to architectures ranging from linear models to
transformers, this simple modification significantly improves out-of-distribution performance (12–15\%) without added computational cost. Critically, we underscore the need to focus on new data generation that improves the connectivity among annotated cell types. Our work suggests this is likely to yield more generalizable algorithms than solely increasing model complexity.
https://doi.org/10.1101/2025.04.23.650210
with Davide D’Ascenzo, Srivatsan Raghavan, Ava Amini, Peter Winter, Lorin Crawford
its infancy. This survey illustrates the recent efforts to broaden these ideas to model spatial interactions among multiple configurations,
each distinguished by a color. It describes advances in this area and prepares the ground for further exploration by mentioning
unresolved questions and promising research avenues while focusing on the overlap with discrete geometry.
arXiv:2405.17920
with Ondrej Draganov, Herbert Edelsbrunner, Morteza Saghafian
for accurate analysis. This paper examines the banana tree data structure, specifically designed to efficiently maintain
persistent homology — a multi-scale topological descriptor — for dynamically changing time series data. We implement
this data structure and conduct an experimental study to assess its properties and runtime for update operations. Our findings indicate that banana trees are highly effective with unbiased random data, outperforming state-of-the-art static algorithms in these scenarios. Additionally, our results show that real-world time series share structural properties with unbiased random walks, suggesting potential practical utility for our implementation.
Accepted at the 41st Symposium on Computational Geometry (SoCG) arXiv:2405.17920
with Lara Ost, Herbert Edelsbrunner
A∖B divided by the length of the minimum spanning tree of A. The question of the supremum, over all sets A, of the maximum,
over all subsets B, is related to the Steiner ratio, and we prove this sup-max is between 2.154 and 2.427. Restricting ourselves
to 2-dimensional lattices, we prove that the sup-max is 2.0, while the inf-max is 1.25. By some margin the most difficult of these results is the upper bound for the inf-max, which we prove by showing that the hexagonal lattice cannot have MST-ratio larger than 1.25.
Published at GD2024
with Ondrej Draganov, Herbert Edelsbrunner, Morteza Saghafian
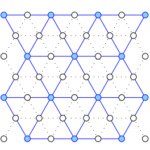
The data structure supports local operations, including the insertion and deletion of an item and the cutting and concatenating of lists,
each in time O(log n + k), in which n is the number of critical items and k is the number of changes in the augmented persistence
diagram.
Published at SODA 2024
with Herbert Edelsbrunner, Monika Henzinger, Lara Ost

Based on persistent homology for images, kernels and cokernels, we design provably stable homological quantifiers that describe the
geometric micro- and macro-structure of how the color classes mingle. These can be efficiently computed using chromatic variants
of Delaunay mosaics and Alpha complexes.
Published at Foundations of Data Science (FoDS)
with Ondrej Draganov, Herbert Edelsbrunner, Morteza Saghafian
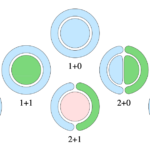
Delaunay mosaic in R^{s+d} that represents how points of different colors mingle. Our main results are bounds on the size of the
chromatic Delaunay mosaic, in which we assume that d and s are constants.
For example, if A is finite with n = #A, and the coloring is random, then the chromatic Delaunay mosaic has O(n⌈d/2⌉ ) cells in expectation. In contrast, for Delone sets and Poisson point processes in R^d, the expected number of cells within a closed ball is only a constant times the number of points in this ball. Furthermore, in R^2 all colorings of a dense set of n points have chromatic Delaunay mosaics of size O(n). This encourages the use of chromatic Delaunay mosaics in applications.
Accepted at DCG
with Ranita Biswas, Ondrej Draganov, Herbert Edelsbrunner, Morteza Saghafian

We prove Euler-type relations, which imply extensions of the classic Dehn-Sommerville relations for convex polytopes to sublevel
sets of the depth function, and we use the relations to extend the expressions for the number of faces of neighborly polytopes to
the number of cells of levels in neighborly arrangements.
Published at the Journal of Applied and Computational Topology, Special Issue: ATMCS10
with Ranita Biswas, Herbert Edelsbrunner, Morteza Saghafian

proofs of theorems about the symmetry of persistence diagrams and the variation of such maps. In particular, we identify branching
points and endpoints of networks as the sole source of asymmetry and relate the cycle basis in persistent homology with a version
of the stable marriage problem. Our analysis provides the foundations of fast algorithms for maintaining collections of interrelated sorted lists together with their persistence diagrams.
Published at the Journal of Applied and Computational Topology, Special Issue: Data Science on Graphs
with Ranita Biswas, Herbert Edelsbrunner, Morteza Saghafian

Delaunay mosaic can be defined by locally maximizing the negative power distance to other such points. We prove that the average
of the two piecewise quadratic functions is piecewise linear, and that all three functions have the same critical points and values.
Discretizing the two piecewise quadratic functions, we get the alpha shapes as sublevel sets of the discrete function on the Delaunay mosaic, and analogous shapes as superlevel sets of the discrete function on the Voronoi tessellation. For the same non-critical value, the corresponding shapes are disjoint, separated by a narrow channel that contains no critical points but the entire level set of the piecewise linear function.
Published at the Journal of Discrete an Computational Geometry
with Ranita Biswas, Herbert Edelsbrunner, Morteza Saghafian
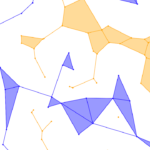
in terms of Morse theoretic quantities for piecewise constant functions on planar arrangements. Specifically, we prove that for a
generic set of n ≥ 5 points in R3,the number of regions in the order-k Voronoi tessellation is Nk−1 –(k/2)n + n, for 1 ≤ k ≤ n − 1,
in which Nk−1 is the sum of Euler characteristics of these function’s first k − 1 sublevel sets. We getsimilar expressions for the vertices, edges, and polygons of the order-k Voronoi tessellation.
Published at the 37th Symposium on Computational Geometry (SoCG)
with Ranita Biswas, Herbert Edelsbrunner, Morteza Saghafian